- Katılım
- 17 Tem 2023
- Mesajlar
- 15,371
- Çözümler
- 1
- Tepki puanı
- 4,396
- Puanları
- 113
- Konum
- ab inferno
- Cinsiyet
- Kadın
Aklınıza ilk gelen yanıt “sıfır” olmuş olabilir ama doğru değil. Sonsuz en büyük rakamsa tersi de en küçük rakam olmalı öyle değil mi? O halde bu sayı sıfırdan büyük bir sayı olmalıdır. Ancak sıfırdan büyük en küçük sayıyı bulmak pek de kolay bir iş değildir.


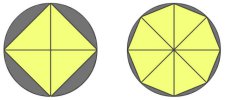
Örneğin; dairenin alan formülünü düşünelim. Kepler dairenin alanını üçgenlere bölerek hesaplamıştır. Basitçe anlatabilmek için adım adım ilerleyelim: Bir dairenin alanını hesaplamak için daireyi dört üçgene böldüğünüzü düşünelim. (Aşağıdaki görselde ki ilk şekle bakın) Bu dört üçgenin alanını hesaplayıp, sonuçları toplarsak dairenin alanını bulabilir miyiz? Yaklaşık bir sonuç buluruz ama resimde de görüldüğü gibi dairenin gri alanları hesaplamaya dahil edilmediğinden sonuç hatalıdır.
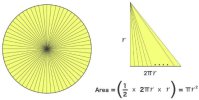
Bu hatayı azaltmak için daireyi 4 üçgene değil, daha fazla üçgene bölebiliriz. Ne kadar çok üçgene bölersek hata o kadar azalacaktır ancak sonsuza kadar bölmeden kusursuz olarak dairenin alanını hesaplamak mümkün olmayacaktır. Sonsuza kadar bölmek de mümkün olmayacağına göre en nihayetinde formül hatalıdır.
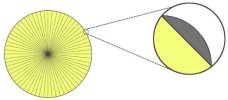
Kuşkusuz Kepler ne kadar ince üçgenler çizerse çizsin yine de tam doğruya ulaşamayacağını biliyordu. Çünkü sonsuza kadar üçgen çizmesi mümkün değildi. Üçgen çizmeyi bıraktığı anda geride hesaplanmamış alanlar kalacaktı. Bu durum matematikçileri rahatsız etse de fizik biliminin ilerlemesi için bu hatayı yok saymamız gerekiyordu.
Leibniz ve Newton tarafından birbirlerinden habersiz bir şekilde geliştirilen kalkülüs (diferansiyel ve integral hesaplamalar) de sonsuzluklar üzerine kurulmuştur.
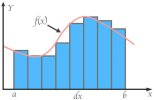
Değişkenler hesabı adı ile de anılan kalkülüs, matematiğin değişim eğrilerinin alanını hesaplayan dalıdır. Örneğin, bir işlevi bütünleştirdiğimizde, esasen çizdiği eğrinin altındaki alanı hesaplarız. Tıpkı bir dairenin alanını hesaplamak gibi eğrinin altında kalan alanı da küçük kusurlara göz yumarak hesaplayabiliriz.

Sonsuzluğun Tuhaflığı
Sonsuzluk, antik çağlardan beri anlamakta zorluk çektiğimiz bir kavram. Sonsuzu anlamak için öncelikle onun bir sayıdan ziyade bir fikir olduğunu anlamalıyız. Sonsuzluk aslında sadece soyutlama ile var olan bir kavramdır. Bunun bir kavram olduğunu daha iyi anlatmak için verilen klasik örneğe bir göz atalım: Sonsuza X diyecek olursak X+1 ne anlama gelir? Sonsuzdan daha büyük bir sonsuzluk mu? Peki ya X+2 o da sonsuzluktan daha da büyük bir sonsuzluk mu? Bu durum küçük sayılar için de aynen geçerlidir. Yani aslında sonsuzluğun tersi de sonsuzluktur. Çünkü sayılar sonsuza kadar büyüdüğü gibi sonsuza kadar küçülür. Sayıların bölünebilir doğası gereği ardışık iki sayı arasında sonsuz sayı vardır. 0 ile 1 arasında yüzlerce, binlerce sayı bulabiliriz. Sonuç olarak sonsuz küçüklük gibi sonsuz büyüklük sadece soyutlama içinde var olabilen kavramlardır. Bu durum matematikçiler için olduğu kadar fizikçiler için de önemlidir.Sonsuz Küçüklük Hataları!
Matematik, fizik alanındaki düşüncelerimizi ifade ettiğimiz bir dildir. Dolayısıyla fizikteki bir tutarsızlıktan söz ettiğimizde, bunu matematik dili ile ifade etmemiz gerekir. Bu nedenle birçok formül, sonsuz küçüklüğün belirsizliğinden kaynaklanan tutarsızlık üzerine kurulmuştur. Aslında matematiğin bütün dalları sonsuz küçüklüğe (infinitezimal) dayanır ki eğer öyle olmasaydı fizik alanında bilimsel ilerleme imkanı ortadan kalkardı.
Örneğin; dairenin alan formülünü düşünelim. Kepler dairenin alanını üçgenlere bölerek hesaplamıştır. Basitçe anlatabilmek için adım adım ilerleyelim: Bir dairenin alanını hesaplamak için daireyi dört üçgene böldüğünüzü düşünelim. (Aşağıdaki görselde ki ilk şekle bakın) Bu dört üçgenin alanını hesaplayıp, sonuçları toplarsak dairenin alanını bulabilir miyiz? Yaklaşık bir sonuç buluruz ama resimde de görüldüğü gibi dairenin gri alanları hesaplamaya dahil edilmediğinden sonuç hatalıdır.

Bu hatayı azaltmak için daireyi 4 üçgene değil, daha fazla üçgene bölebiliriz. Ne kadar çok üçgene bölersek hata o kadar azalacaktır ancak sonsuza kadar bölmeden kusursuz olarak dairenin alanını hesaplamak mümkün olmayacaktır. Sonsuza kadar bölmek de mümkün olmayacağına göre en nihayetinde formül hatalıdır.

Kuşkusuz Kepler ne kadar ince üçgenler çizerse çizsin yine de tam doğruya ulaşamayacağını biliyordu. Çünkü sonsuza kadar üçgen çizmesi mümkün değildi. Üçgen çizmeyi bıraktığı anda geride hesaplanmamış alanlar kalacaktı. Bu durum matematikçileri rahatsız etse de fizik biliminin ilerlemesi için bu hatayı yok saymamız gerekiyordu.

Leibniz ve Newton tarafından birbirlerinden habersiz bir şekilde geliştirilen kalkülüs (diferansiyel ve integral hesaplamalar) de sonsuzluklar üzerine kurulmuştur.

Değişkenler hesabı adı ile de anılan kalkülüs, matematiğin değişim eğrilerinin alanını hesaplayan dalıdır. Örneğin, bir işlevi bütünleştirdiğimizde, esasen çizdiği eğrinin altındaki alanı hesaplarız. Tıpkı bir dairenin alanını hesaplamak gibi eğrinin altında kalan alanı da küçük kusurlara göz yumarak hesaplayabiliriz.









